El descenso del gradiente: la brújula del Machine Learning

En este post analizaremos uno de los algoritmos más fundamentales tanto en el ámbito del Machine Learning y Deep Learning como la optimización matemática: el descenso del gradiente. Como científicos de datos, es imperativo comprender con rigurosidad los algoritmos que empleamos en nuestro día a día. Para ello, abordaremos qué es el descenso del gradiente, su formulación matemática y los desafíos que presenta.

¡Comenzamos!

En el campo del Machine Learning y la optimización matemática, el descenso del gradiente destaca como uno de los algoritmos más empleados debido a su eficiencia, robustez y versatilidad. Este algoritmo, esencial para la convergencia de modelos, representa una herramienta muy poderosa para encontrar el camino hacia el óptimo en un espacio de parámetros. El concepto de «óptimo» en matemáticas es fundamental y ampliamente empleado, ya que representa un estado de eficiencia máxima según ciertos criterios establecidos.

En este artículo, desentrañaremos el descenso del gradiente utilizando una analogía común para facilitar su comprensión. Además, examinaremos detalladamente las bases matemáticas de este algoritmo y los beneficios que aporta a nuestros proyectos de Machine Learning.

El descenso del gradiente es un algoritmo de optimización empleado para encontrar el mínimo de una función. En el ámbito de la optimización, el objetivo es identificar la solución óptima a un problema específico.

Para que todos podamos entender la definición anterior de una forma intuitiva, supongamos que estamos perdidos en una montaña, en medio de una niebla densa, similar a la que se puede observar en la imagen siguiente, y solo podemos ver la pendiente del terreno bajo nuestros pies. Queremos descender y llegar al valle lo más rápido posible. ¿Cómo lo haríamos?

Pues bien, una buena estrategia para llegar al fondo del valle es ir cuesta abajo en la dirección de la pendiente más empinada. Esta analogía refleja la esencia del algoritmo del descenso del gradiente, que se asemeja a un guía que nos indica la ruta más directa para descender la montaña.

Primero, el algoritmo mide la pendiente del terreno en el punto donde nos encontramos, lo cual representa el gradiente. Luego, avanza en la dirección en la que la pendiente es más pronunciada, justificando así el término descenso. Este proceso se repite tantas veces como sea necesario hasta alcanzar el fondo del valle. Una vez que el gradiente alcanza el valor cero, hemos alcanzado el mínimo y, por lo tanto, el óptimo. En otras palabras, hemos llegado al punto donde el terreno es llano y sin inclinación.

Ahora, analizaremos en detalle la expresión matemática de los conceptos mencionados anteriormente y su importancia en el campo del Machine Learning.

Hablar sobre este algoritmo sin explorar las matemáticas subyacentes es equiparable a jugar al ajedrez sin conocer las reglas o estrategias básicas del juego. Sin ese conocimiento, nuestras habilidades estarían limitadas y, en el caso del descenso del gradiente, no podríamos emplearlo de manera efectiva al no comprender su funcionamiento interno.

Matemáticamente, el descenso del gradiente se expresa como sigue:

Dada una función f(θ) , donde θ es un vector de parámetros, el descenso del gradiente se basa en actualizar iterativamente θ de acuerdo con la siguiente fórmula matemática:

θ= θ – α∇ f(θ)

Donde:

• ∇f(θ) es el gradiente de la función  evaluada en el punto , que representa la dirección de máximo incremento de la función en ese punto.
• α es la tasa de aprendizaje, un hiperparámetro que controla el tamaño de los pasos que da el algoritmo en cada iteración.

Como ya adelantamos, el objetivo del descenso del gradiente es encontrar el mínimo de la función f ajustando θ de manera que la función tenga un valor lo más bajo posible. Este proceso se repite hasta que se alcance una convergencia, es decir, cuando los cambios en θ son muy pequeños o cuando la función alcanza un valor mínimo dentro de un margen de tolerancia predefinido.

Es importante notar que el término α∇ f(θ) se resta de θ porque el objetivo es moverse contra el gradiente, hacia el mínimo local.

En el siguiente vídeo se muestra el funcionamiento de este algoritmo. En la práctica, empezamos inicializando θ con valores aleatorios. Luego, mejoramos estos valores paso a paso, intentando minimizar la función f hasta que el algoritmo converge en un mínimo.

Como ya adelantamos anteriormente, la tasa de aprendizaje, representada por α es un hiperparámetro crucial en el descenso del gradiente. Esta determina la magnitud de los pasos que damos en cada iteración para actualizar los parámetros de θ con el objetivo de minimizar la función f. Una tasa de aprendizaje adecuada es fundamental para el éxito del algoritmo

Si la tasa de aprendizaje es demasiado pequeña, entonces el algoritmo tendrá que pasar por muchas iteraciones para converger, lo cual puede ralentizar el proceso de optimización. El siguiente vídeo muestra esta problemática.

Sin embargo, si la tasa de aprendizaje es demasiado alta, en un intento por encontrar el punto óptimo, el algoritmo puede oscilar alrededor del mínimo o incluso divergir, lo que significa que nunca alcanzaría la solución óptima.

En el contexto del aprendizaje automático, el algoritmo del descenso del gradiente se utiliza para ajustar los parámetros de un modelo de Machine Learning de manera iterativa, con el objetivo de minimizar el error de predicción. Consiste en calcular la dirección y magnitud en la que deben ajustarse los parámetros para reducir la discrepancia entre las predicciones del modelo y los valores reales. En otras palabras, busca determinar cómo modificar los parámetros del modelo para minimizar su diferencia respecto a la salida deseada.

Este error se conoce como la función de coste. La función de coste representa la discrepancia entre el valor predicho y el valor real, es decir, mide cuánto difieren las predicciones del modelo de los valores reales.

Cuanto menor sea esta discrepancia, mejor será el rendimiento del modelo. Por lo tanto, el objetivo principal del descenso del gradiente es minimizar esta función de coste, es decir, encontrar los parámetros del modelo que reduzcan al máximo esta discrepancia. Este proceso iterativo de ajuste de parámetros continúa hasta que se alcanza una convergencia aceptable, es decir, cuando la función de coste ya no disminuye significativamente o cuando se cumple algún otro criterio de detención predefinido. Durante cada iteración, el algoritmo del descenso del gradiente calcula el gradiente de la función de coste con respecto a los parámetros del modelo, lo que indica la dirección y la magnitud en la que deben actualizarse los parámetros para reducir el error de predicción.
Una función de coste comúnmente utilizada tanto en problemas de regresión, redes neuronales o aprendizaje por refuerzo es el error cuadrático medio (MSE, por sus siglas en inglés), que calcula la media de las diferencias al cuadrado entre las predicciones y los valores reales.

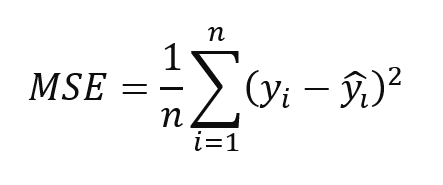
Donde:

• n es el número total de observaciones.
• yᵢ es el valor observado para i-ésima observación.
• ŷᵢ es el valor predicho para i-ésima observación.

Existen otras funciones de coste en función del problema que buscamos resolver, pero su análisis no está dentro del objetivo de este artículo.

Aunque el descenso del gradiente es un algoritmo muy potente, también presenta desafíos.

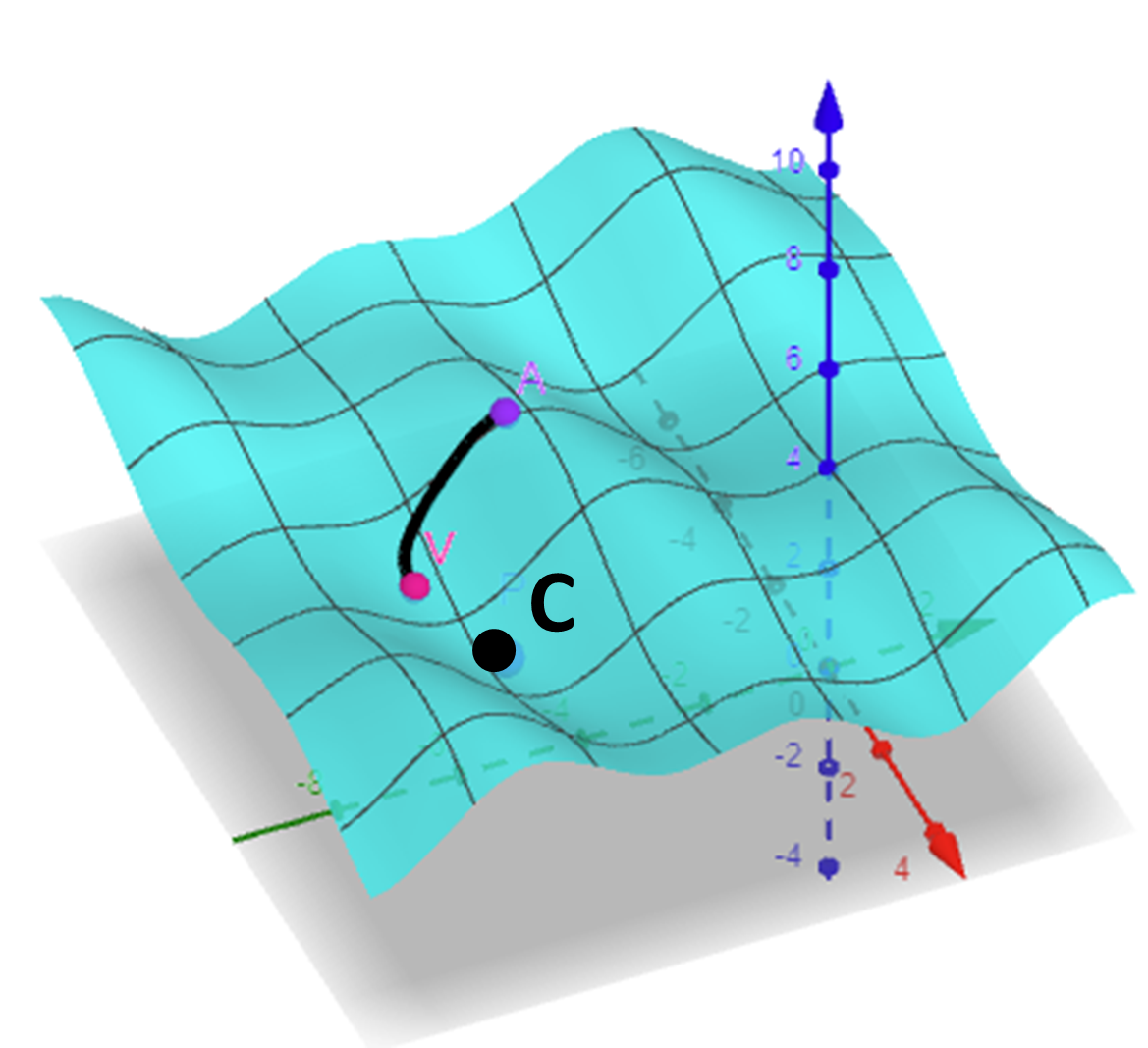
Un riesgo notable es quedar atrapado en óptimos locales, donde la función de pérdida se minimiza, pero no de forma global. Para ilustrarlo, consideremos al montañista del primer ejemplo descendiendo por la montaña, donde dicha montaña representa la función de pérdida que se está optimizando. A medida que el montañista desciende, puede encontrarse con valles secundarios (óptimos locales) en vez de alcanzar el valle más profundo (óptimo global). Esto ejemplifica cómo el descenso del gradiente puede quedar atrapado en óptimos locales en lugar de alcanzar el óptimo global deseado.

En la imagen siguiente podemos ver representado lo anterior. Es decir, el montañista se encuentra en el punto A y desciende hasta el punto V que es un óptimo local pero no un óptimo global, representado por el punto C.

Otra problemática importante relacionada con el descenso del gradiente es el tiempo de convergencia. Debido a la naturaleza iterativa del algoritmo, puede requerir muchas iteraciones para alcanzar la convergencia, especialmente en conjuntos de datos grandes o cuando la función de coste presenta muchas irregularidades o mínimos locales. El tiempo de convergencia es un factor crítico a considerar en el entrenamiento de modelos de Machine Learning, ya que afecta directamente el tiempo necesario para obtener resultados aceptables. Un tiempo de convergencia largo puede resultar en un proceso de entrenamiento lento y costoso computacionalmente, lo que puede ser impracticable en situaciones donde se requiere una respuesta rápida o recursos limitados.

En definitiva, hemos aprendido que el descenso del gradiente no solo es un algoritmo clave en el arsenal de herramientas de Machine Learning, sino que también representa un ejemplo de cómo las matemáticas y el aprendizaje automático se entrelazan en el mundo de la ciencia de datos. Su comprensión y aplicación nos permiten no solo optimizar modelos de manera eficiente, sino también profundizar en los fundamentos matemáticos subyacentes que impulsan el Machine Learning.